Casio fx-7400G PLUS - Handbuch (Seite 58)

44
Kapitel 3 Differentialrechnungen
• Um Differentialrechnungen auszuführen, zuerst das Options-Menü anzeigen und
danach die in der nachfolgenden Formel gezeigten Werte eingeben.
K2(CALC)[
1( d / dx ) f(x) , a , ∆ x )
Nachfolgend ist das Eingabeformat für Differentiale aufgeführt:
In dieser Definition wird der unendlich kleine Wert durch einen ausreichend kleinen
Wert
∆ x , ersetzt, wobei sich dieser Wert in der Nähe von f ' (a) befindet, der wie folgt
berechnet wird:
Um die bestmögliche Genauigkeit zu erhalten, verwendet diese Einheit die
Zentraldifferenz, um Differentialrechnungen auszuführen. Nachfolgend ist die
Zentraldifferenz dargestellt.
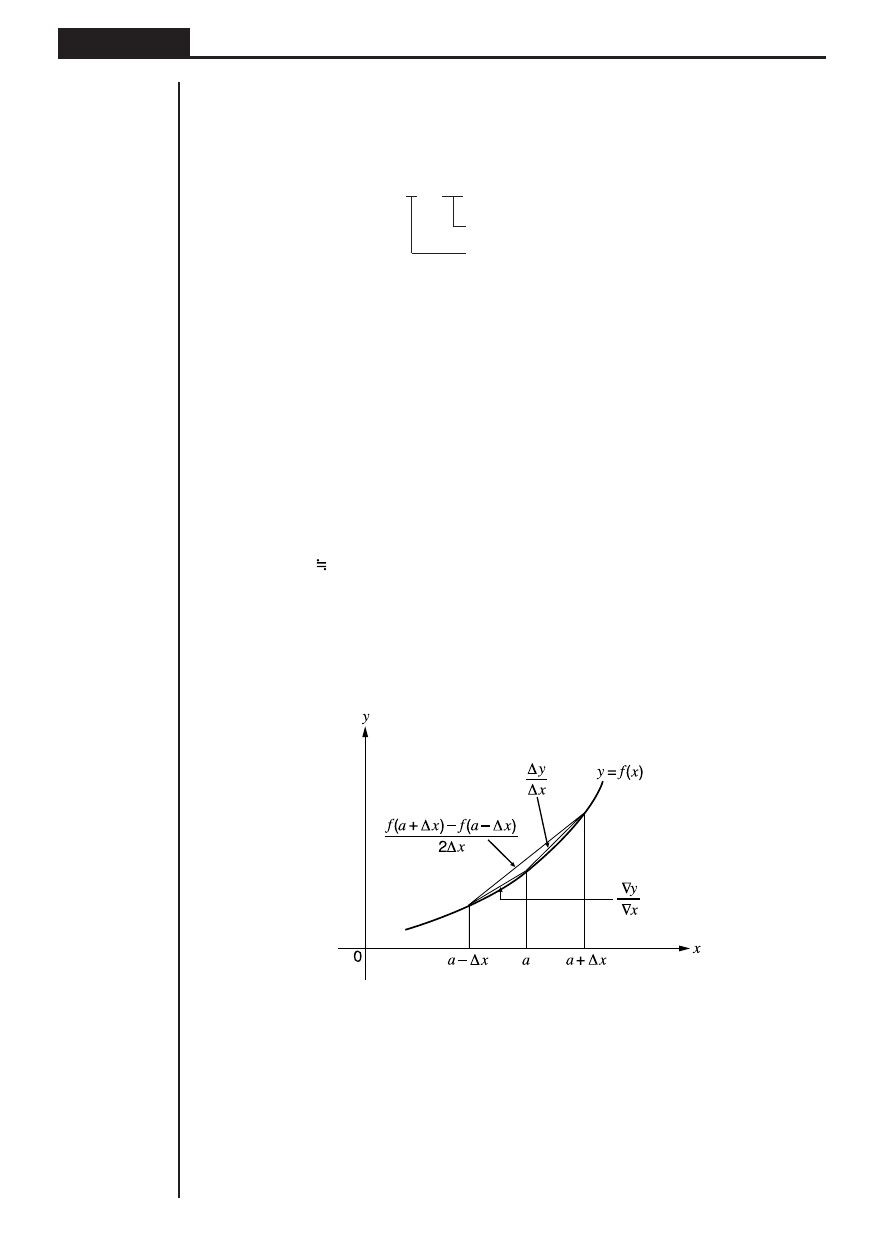
Die Neigungen an Punkt a und Punkt a + ∆ x , sowie an Punkt a und Punkt a – ∆ x in
der Funktion y = f(x) sind wie folgt:
In der obigen Gleichung wird
∆ y /
∆ x als die Vorwärtsdifferenz bezeichnet, wogegen
∇ y /
∇ x als die Rückwärtsdifferenz bezeichnet wird. Um die Differentiale zu berech-
nen, verwendet die Einheit den Durchschnitt zwischen den Werten von
∆ y /
∆ x and
∇ y /
∇ x , wodurch eine höhere Genauigkeit für die Differentiale erhalten wird.
f (a +
∆x) – f (a)
f '(a) = lim –––––––––––––
∆x
∆x→0
f (a +
∆x) – f (a)
f '(a) –––––––––––––
∆x
d
d/dx ( f (x), a,
∆x) ⇒ ––– f (a)
dx
Erhöhung/Verminderung von x
Punkt für den Sie das Differential bestimmen
möchten.
f (a +
∆x) – f (a) ∆ y f (a) – f (a –
∆x) ∇ y
––––––––––––– = ––– , ––––––––––––– = –––
∆x ∆x ∆x ∇x