Definition eines normierten vektors – HEIDENHAIN iTNC 530 (340 49x-02) Benutzerhandbuch
Seite 185
HEIDENHAIN iTNC 530
185
5.4 Dr
eidimensionale W
e
rk
z
e
ug-K
o
rr
ekt
ur (Sof
tw
ar
e-Option
2)
Definition eines normierten Vektors
Ein normierter Vektor ist eine mathematische Größe, die einen Betrag
von 1 und eine beliebige Richtung hat. Bei LN-Sätzen benötigte die
TNC bis zu zwei normierte Vektoren, einen um die Richtung der Flä-
chennormalen und einen weiteren (optionalen), um die Richtung der
Werkzeug-Orientierung zu bestimmen. Die Richtung der Flächennor-
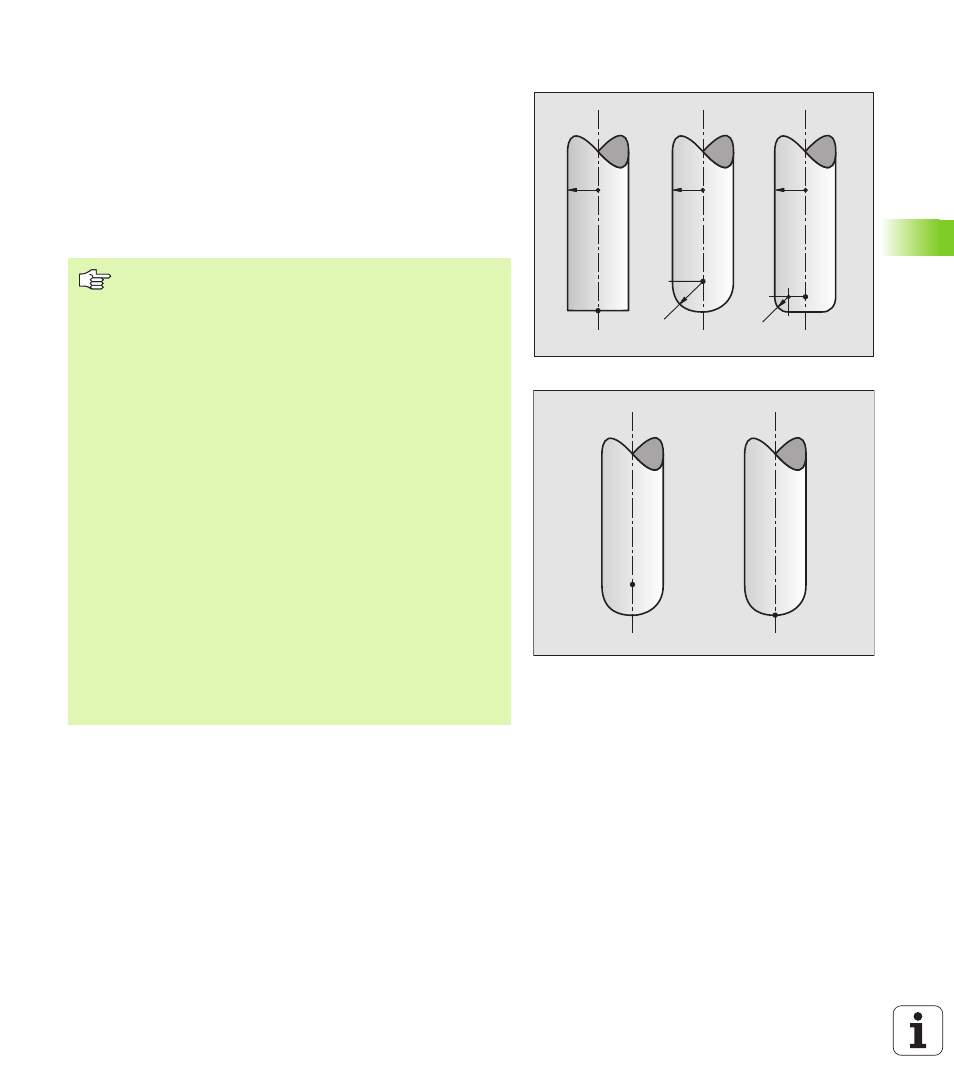
malen ist durch die Komponenten NX, NY und NZ festgelegt. Sie weist
beim Schaft- und Radiusfräser senkrecht von der Werkstück-Oberflä-
che weg hin zum Werkzeug-Bezugspunkt P
T
, beim Eckenradiusfräser
durch P
T
‘ bzw. P
T
(Siehe Bild). Die Richtung der Werkzeug-Orientie-
rung ist durch die Komponenten TX, TY und TZ festgelegt
Die Koordinaten für die Position X,Y, Z und für die Flächen-
normalen NX, NY, NZ, bzw. TX, TY, TZ, müssen im NC-
Satz die gleiche Reihenfolge haben.
Im LN-Satz immer alle Koordinaten und alle Flächennor-
malen angeben, auch wenn sich die Werte im Vergleich
zum vorherigen Satz nicht geändert haben.
TX, TY und TZ muss immer mit Zahlenwerten definiert
sein. Q-Parameter sind nicht erlaubt.
Normalenvektoren grundsätzlich immer auf 7 Nachkom-
mastellen berechnen und ausgeben, um Vorschubeinbrü-
che während der Bearbeitung zu vermeiden.
Die 3D-Korrektur mit Flächennormalen ist für Koordinaten-
angaben in den Hauptachsen X, Y, Z gültig.
Wenn Sie ein Werkzeug mit Übermaß (positive Delta-
werte) einwechseln, gibt die TNC eine Fehlermeldung
aus. Die Fehlermeldung können Sie mit der M-Funktion
M107
unterdrücken (siehe „Voraussetzungen für NC-Sätze
mit Flächennormalen-Vektoren und 3D-Korrektur”, Seite
179).
Die TNC warnt nicht mit einer Fehlermeldung, wenn
Werkzeug-Übermaße die Kontur verletzen würden.
Über den Maschinen-Parameter 7680 legen Sie fest, ob
das CAD-System die Werkzeug-Länge über Kugelzentrum
P
T
oder Kugelsüdpol P
SP
korrigiert hat (siehe Bild).
P
T
R
R
R
R2
P
T
P
T
R2
P
T
'
P
T
P
SP