HEIDENHAIN TNC 640 (34059x-05) - Handbuch (Seite 476)

Programmieren: Mehrachs-Bearbeitung
12.6 Dreidimensionale Werkzeugkorrektur (Option #9)
12
476
TNC 640 | Benutzer-Handbuch HEIDENHAIN-Klartext-Dialog | 1/2015
Definition eines normierten Vektors
Ein normierter Vektor ist eine mathematische Größe, die einen
Betrag von 1 und eine beliebige Richtung hat. Bei LN-Sätzen
benötigte die TNC bis zu zwei normierte Vektoren, einen
um die Richtung der Flächennormalen und einen weiteren
(optionalen), um die Richtung der Werkzeugorientierung zu
bestimmen. Die Richtung der Flächennormalen ist durch die
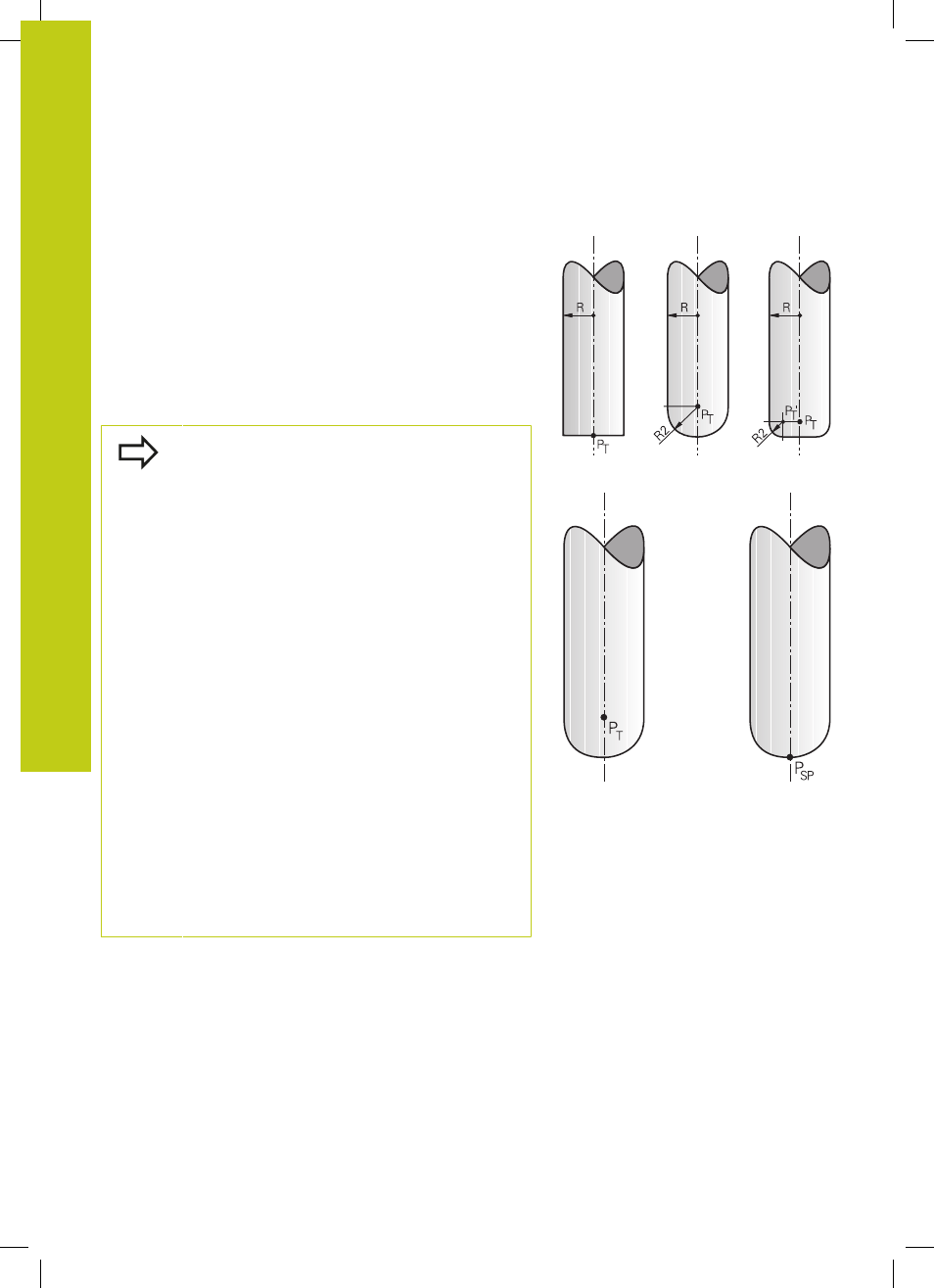
Komponenten NX, NY und NZ festgelegt. Sie weist beim Schaft-
und Radiusfräser senkrecht von der Werkstück-Oberfläche weg hin
zum Werkzeugbezugspunkt PT, beim Eckenradiusfräser durch PT‘
bzw. PT (Siehe Bild). Die Richtung der Werkzeugorientierung ist
durch die Komponenten TX, TY und TZ festgelegt
Die Koordinaten für die Position X,Y, Z und für die
Flächennormalen NX, NY, NZ, bzw. TX, TY, TZ,
müssen im NC-Satz die gleiche Reihenfolge haben.
Im LN-Satz immer alle Koordinaten und alle
Flächennormalen angeben, auch wenn sich die Werte
im Vergleich zum vorherigen Satz nicht geändert
haben.
TX, TY und TZ muss immer mit Zahlenwerten
definiert sein. Q-Parameter sind nicht erlaubt.
Normalenvektoren möglichst genau berechnen
und mit entsprechend vielen Nachkommastellen
ausgeben, um Vorschubeinbrüche während der
Bearbeitung zu vermeiden.
Die 3D-Korrektur mit Flächennormalen ist für
Koordinatenangaben in den Hauptachsen X, Y, Z
gültig.
Wenn Sie ein Werkzeug mit Übermaß (positive
Deltawerte) einwechseln, gibt die TNC eine
Fehlermeldung aus. Die Fehlermeldung können
Sie mit der M-Funktion
M107 unterdrücken (siehe
"Definition eines normierten Vektors", Seite 476).
Die TNC warnt nicht mit einer Fehlermeldung, wenn
Werkzeugübermaße die Kontur verletzen würden.
Über den Maschinenparameter toolRefPoint legen
Sie fest, ob das CAM-System die Werkzeuglänge
über Kugelzentrum PT oder Kugelsüdpol PSP
korrigiert hat (siehe Bild).