K absolutwert und argument, K konjugiert komplexe zahlen – Casio fx-9750GA PLUS Benutzerhandbuch
Seite 53
2-6-2
Rechnen mit komplexen Zahlen
k Absolutwert und Argument
[OPTN] - [CPLX] - [Abs]/[Arg]
Der Rechner interpretiert jede komplexe Zahl in der Form
a
+
b i
als Koordinate in der
Gauß'schen Zahlenebene und berechnet den Absolutwert
⎮ Z ⎮ und das Argument (arg).
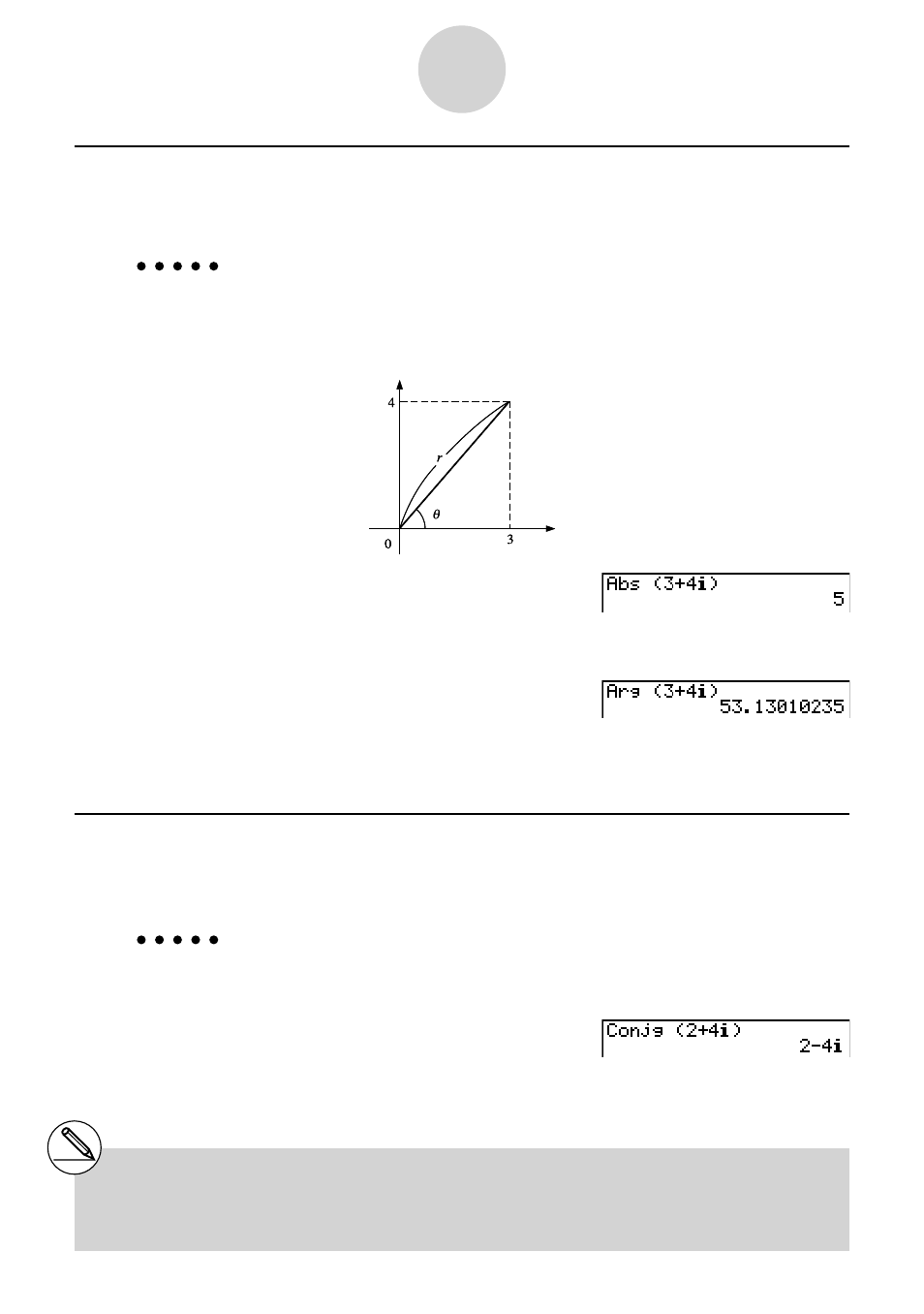
Beispiel
Zu berechnen sind der Absolutwert (
r
) und das Argument (
θ ) für die
komplexe Zahl 3 + 4
i
, wobei der Winkelmodus auf Altgrad eingestellt
werden soll.
Imaginäre
Achse
Reelle Achse
A
K3(CPLX) 2(Abs)
(d+e1(
i
)
)w
(Berechnung des Absolutwertes)
A
K3(CPLX) 3(Arg)
(d+e1(
i
)
)w
(Berechnung des Arguments (Winkels))
k Konjugiert komplexe Zahlen
[OPTN] - [CPLX] - [Conj]
Eine komplexe Zahl der Form
a
+
b i
wird in die konjugiert komplexe Zahl der Form
a
–
b i
umgeformt.
Beispiel
Zu berechnen ist die konjugiert komplexe Zahl zur komplexen Zahl
2 + 4
i
A
K3(CPLX) 4(Conj)
(c+e1(
i
)
)w
# Das Ergebnis der Argumentberechnung hängt
vom aktuell eingestellten Winkelmodus (Altgrad,
Bogenmaß, Neugrad) ab.