U quadrieren einer (quadratischen) matrix – Casio fx-9750GA PLUS Benutzerhandbuch
Seite 70
2-8-13
Matrizenrechnung
u Matrix-Inversion (einer regulären quadratischen Matrix)
[OPTN] - [MAT] - [
x
-1
]
Beispiel
Die folgende Matrix ist zu invertieren:
Matrix A =
1 2
3 4
K2(MAT) 1(Mat)
av(A) !
)(
x
–1
) w
u Quadrieren einer (quadratischen) Matrix
[OPTN] - [MAT] - [
x
2
]
Beispiel
Die folgende Matrix ist mit sich selbst zu multiplizieren, d. h. zu
quadrieren:
Matrix A =
1 2
3 4
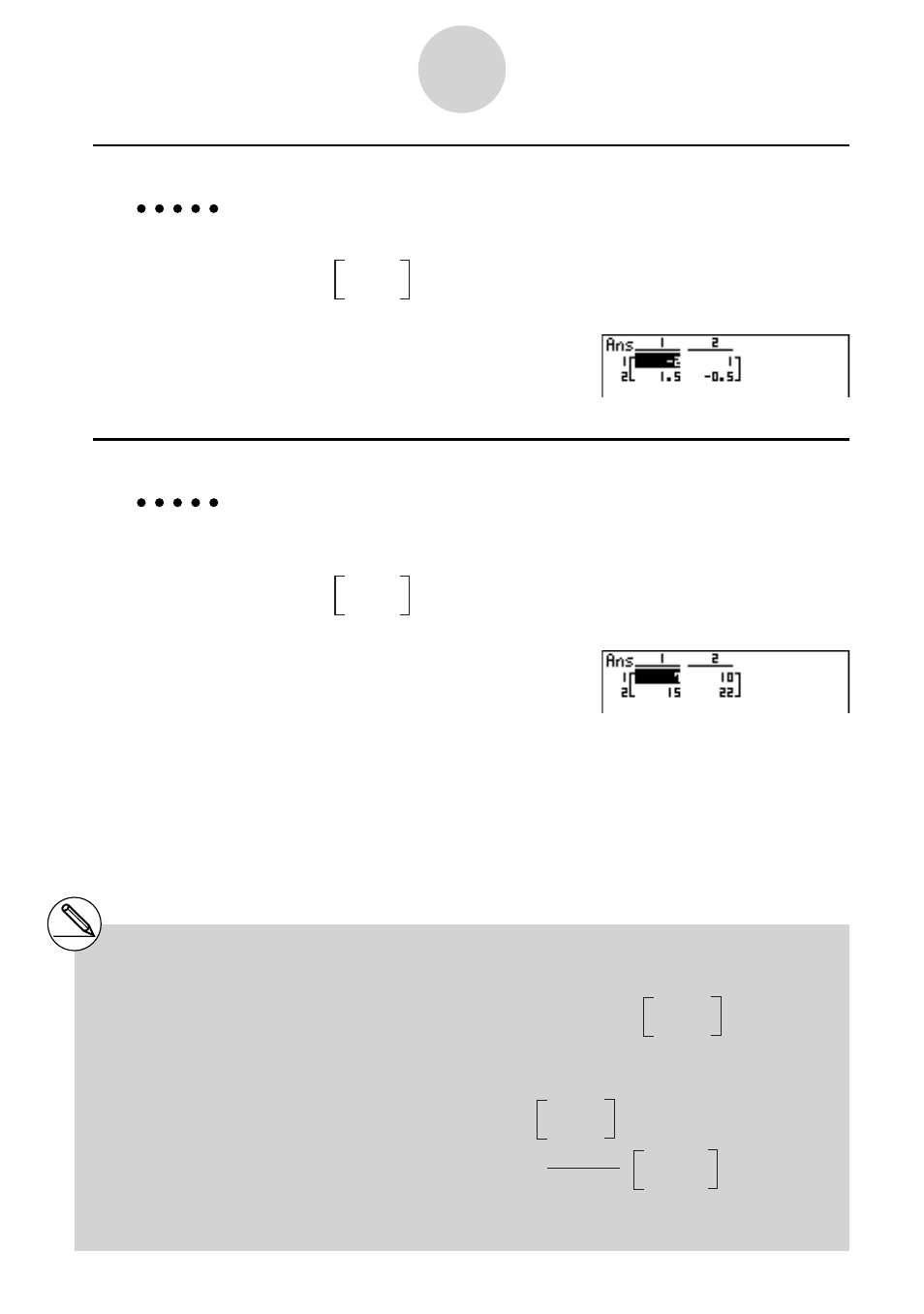
K2(MAT) 1(Mat) av(A) xw
# Nur reguläre quadratische Matrizen (mit einer
von Null verschiedenen Determinante) können
invertiert werden. Falls das Invertieren einer
nicht quadratischen oder nicht regulären
Matrix versucht wird, kommt es zu einer
Fehlermeldung.
# Eine Matrix mit der Determinante 0 (singuläre
Matrix) kann nicht invertiert werden. Falls das
Invertieren einer Matrix mit der Determinante
0 versucht wird, kommt es zu einer
Fehlermeldung.
# Die Rechengenauigkeit wird bei einer Matrix-
Inversion mit einer Determinante nahe 0
möglicher Weise beeinträchtigt.
# Eine Matrix kann nur invertiert werden, wenn sie
die folgenden Bedingungen erfüllt:
Mit der folgenden Formel wird für eine Matrix A
die inverse Matrix A
–1
berechnet:
Man beachte, dass ad – bc
G
0 ist.
A A
–1
= A
–1
A = E =
1 0
0 1
A =
a b
c d
A
–1
=
1
ad – bc
d –b
–c
a