Casio CFX-9850GB PLUS - Handbuch (Seite 329)

301
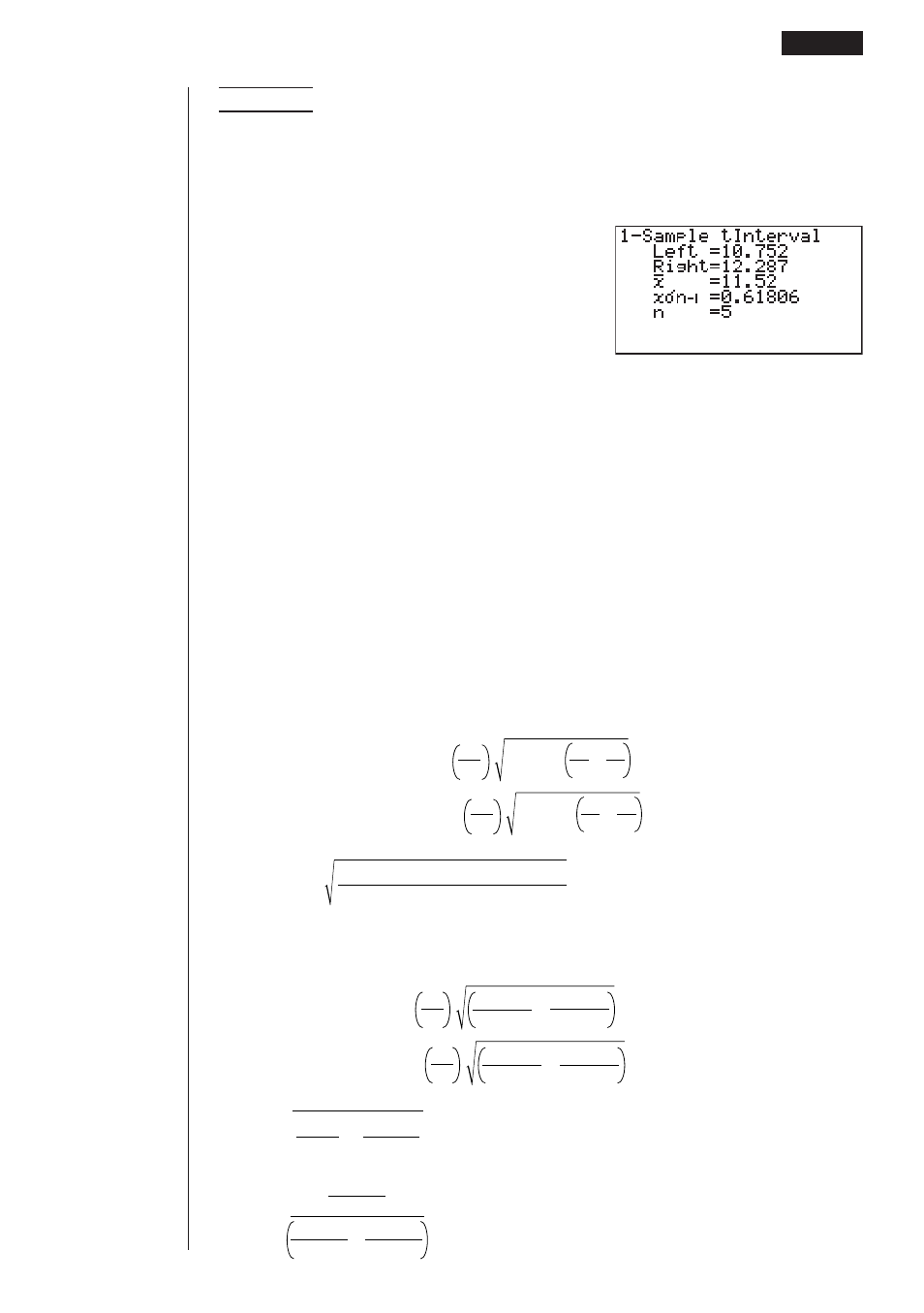
Beispiel Zu berechnen ist der 1-Proben t -Bereich für eine Liste von
Daten.
Für dieses Beispiel wollen wir den 1-Proben t -Bereich für die
Daten = {11,2, 10,9, 12,5, 11,3, 11,7} erhalten, wenn C-Level =
0,95 ist.
1(List)c
a.jf
w
1(List1)c
1(1)c
1(CALC)
Left ................. Untere Bereichsgrenze (linke Kante)
Right ............... Obere Bereichsgrenze (rechte Kante)
o ..................... Sample-Durchschnitt
x
σ
n -1
................ Sample-Standardabweichung
n ..................... Sample-Größe
u u u u u2-Proben t-Bereich (2-Sample t Interval)
Der 2-Proben t -Bereich berechnet die Sicherheitsgrenze für die Differenz
zwischen zwei Mittelwerten der Population, wenn beide Population-
Standardabweichungen unbekannt sind. Das
t -Intervall wird für die t -Verteilung
verwendet.
Der folgende Vertrauensbereich trifft zu, wenn Pooling wirksam ist.
Der Wert 100 (1–
α
) % entspricht der Sicherheitsschwelle.
Left = ( o
1
– o
2
)– t
α
2
Right = ( o
1
– o
2
)+ t
α
2
n
1
+n
2
–2 n
1
1 +
n
2
1
x
p n –1
2
σ
n
1
+n
2
–2 n
1
1 +
n
2
1
x
p n –1
2
σ
Der folgende Vertrauensbereich trifft zu, wenn Pooling nicht wirksam ist.
Der Wert 100 (1–
α
) % entspricht der Sicherheitsschwelle.
Left = ( o
1
– o
2
)– t
df
α
2
Right = ( o
1
– o
2
)+ t
df
α
2
+
n
1
x
1 n–1
2
σ
n
2
x
2 n–1
2
σ
+
n
1
x
1 n–1
2
σ
n
2
x
2 n–1
2
σ
C =
df =
1
C 2
n
1
–1
+
(1–C ) 2
n
2
–1
+
n
1
x
1 n–1
2
σ
n
1
x
1 n–1
2
σ
n
2
x
2 n–1
2
σ
Vertrauensbereich
18 - 7
x
p n –1
=
σ
n
1
+ n
2
– 2
(n
1
–1)x
1 n –1
2 +(n
2
–1) x
2 n –1
2
σ σ