K potenz-regression (quasilineare regression), K sinus-regression (nichtlineare regression) – Casio FX-CG10 Benutzerhandbuch
Seite 213
6-19
k Potenz-Regression (quasilineare Regression)
Die Potenzregression beschreibt die abhängige Variable
y
als Potenzfunktion von
x
. Die
Standardformel für die Potenzregression lautet
y
=
a
×
x
b
, so dass man In
y
= In
a
+
b
× In
x
erhält, wenn beide Seiten der Modellgleichung logarithmiert werden. Falls
man dann die Transformationen X = In
x
, Y = In
y
und A = ln
a
benutzt, erhält man die Formel
Y = A +
b
X für die lineare Regression (quasilineare Regression).
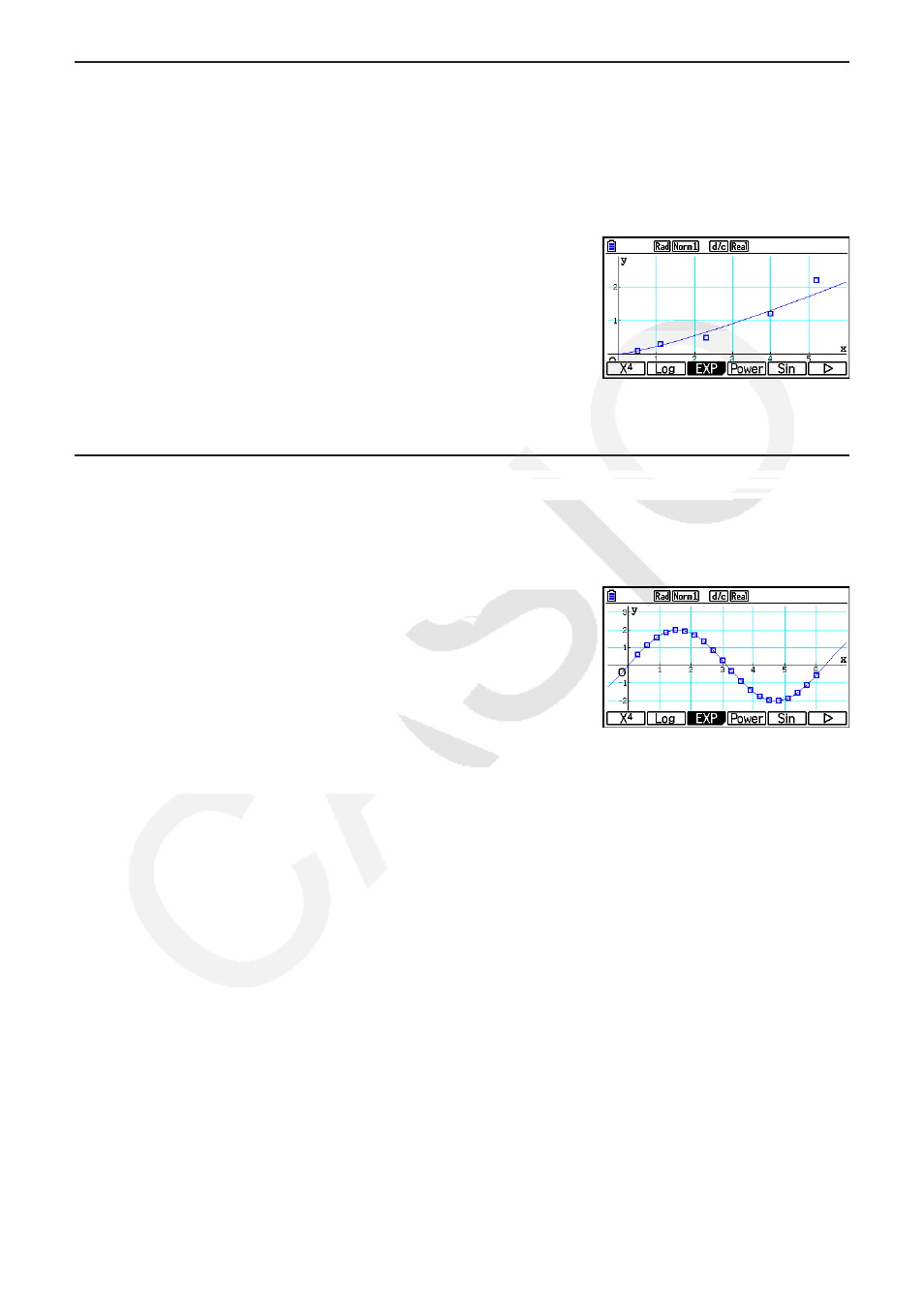
1(CALC) 6( g) 4(Power)
6(DRAW)
Nachfolgend ist die Modellformel für die Potenz-Regression
aufgeführt.
y
=
a
·
x
b
a
.............. Regressionskoeffizient
b
.............. Regressionsexponent
k Sinus-Regression (nichtlineare Regression)
Die Sinus-Regression wird am besten für zyklische Daten angewendet, die eine Periodizität
erkennen lassen.
Nachfolgend ist die Modellformel für die Sinus-Regression aufgeführt.
y
=
a
·sin(
bx
+
c
) +
d
1(CALC) 6( g) 5(Sin)
6(DRAW)
Beim Zeichnen einer Sinus-Regressionsgrafik werden die Winkeleinheiten des Rechners
automatisch auf Rad (das Bogenmaß) eingestellt. Die Winkeleinheit ändert sich nicht, wenn
Sie eine Sinus-Regression ohne das Zeichnen einer Grafik ausführen.
• Bestimmte Datenlisten verursachen eine sehr lange Zeitspanne für die Berechnung, da die
Regressionsparameter iterativ ermittelt werden. Dies stellt jedoch keinen Fehlbetrieb des
Rechners dar.